[コンプリート!] 図形 の 重心 の 求め 方 212384-図形 の 重心 の 求め 方
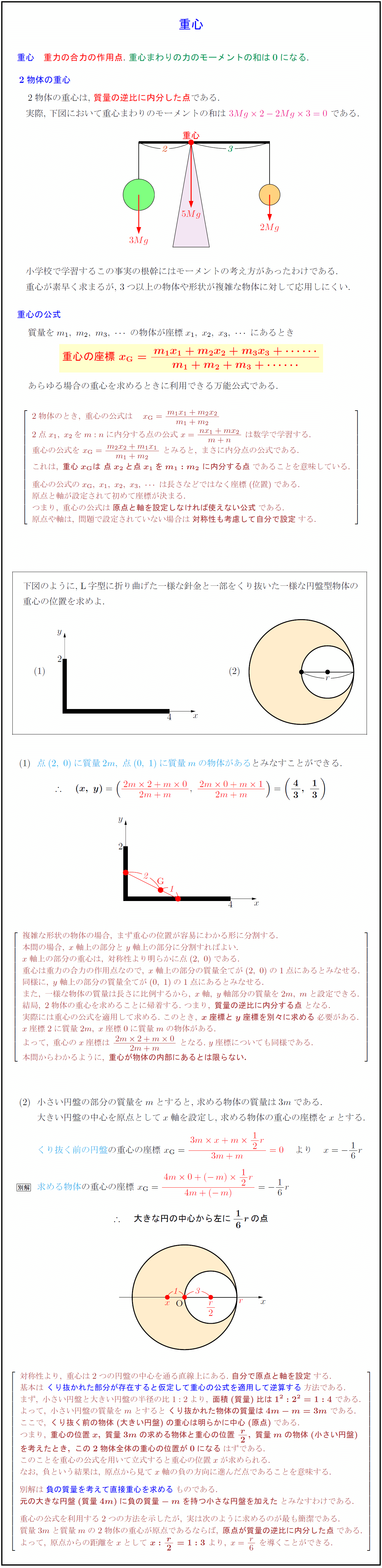
高校物理 剛体の力学 重心 L字型物体 一部がくり抜かれた物体 重心の公式 受験の月
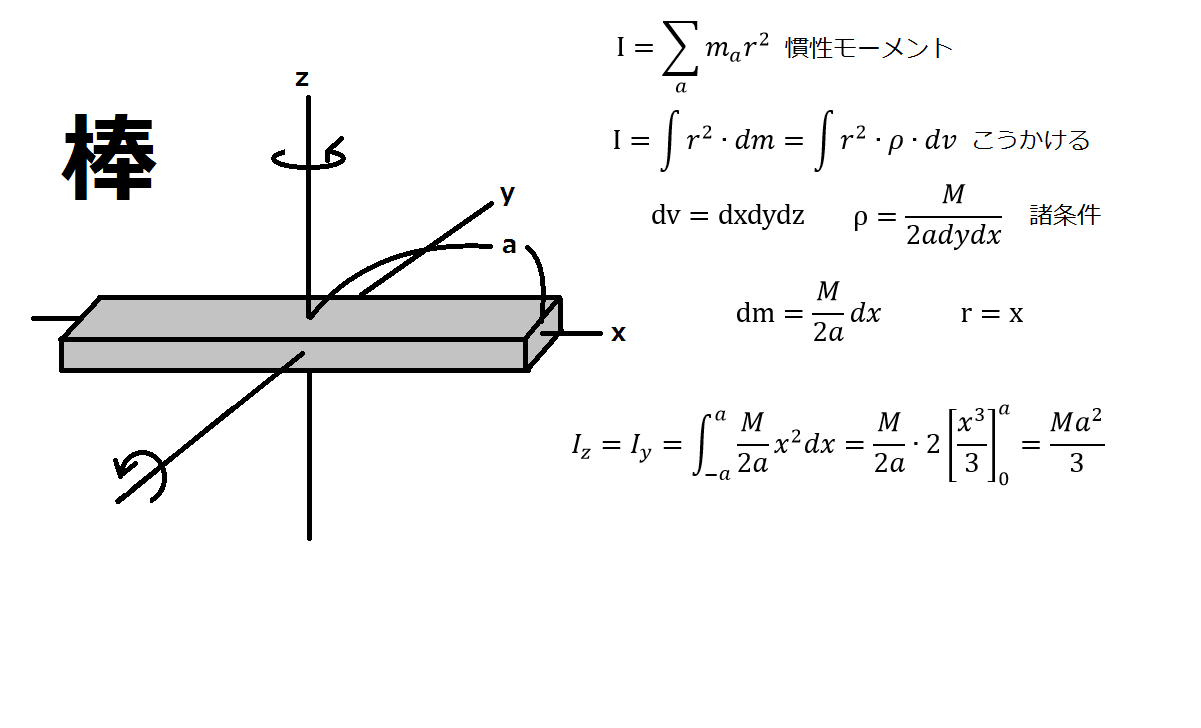
重心 高校物理では, 質量はあるが大きさは無視できる という 質点 についての議論がもっぱらである しかし, 現実の物体はゼロでない大きさを持ち, 物体内部で質量の分布に 斑 ( むら ) もあるであろう このような現実的な物体を議論する場合において図心を求めるための下準備をしましょう ①まず、計算しやすくするため3つの長方形に分割します。 ②分割した長方形の面積を求めます。 a=5m×2m=10㎡ b=2m×4m=8㎡ c=10m×2m=㎡ ③X軸、Y軸から中心(図心)まで距離を求めておきます。
図形 の 重心 の 求め 方
図形 の 重心 の 求め 方- 以下のプログラムは重心を求めるプログラムなそうなのですが、例えば検出した円や四角形の重心を取るとします。ここで質問なのですが、以下のプログラムでどうやって重心を求めているのでしょうか?アルゴリズム C言語・C・C# 解決済 教えて!goo 分布の重心 マ ラソン 大会では大勢の人が一度にスタートを切って走り始めます.スタートして からし ばらく経つと,選手は皆走る速さに違いがあるので,それぞれの選手が走っている場所はばらばらになっています.このとき,選手は平均するとどの
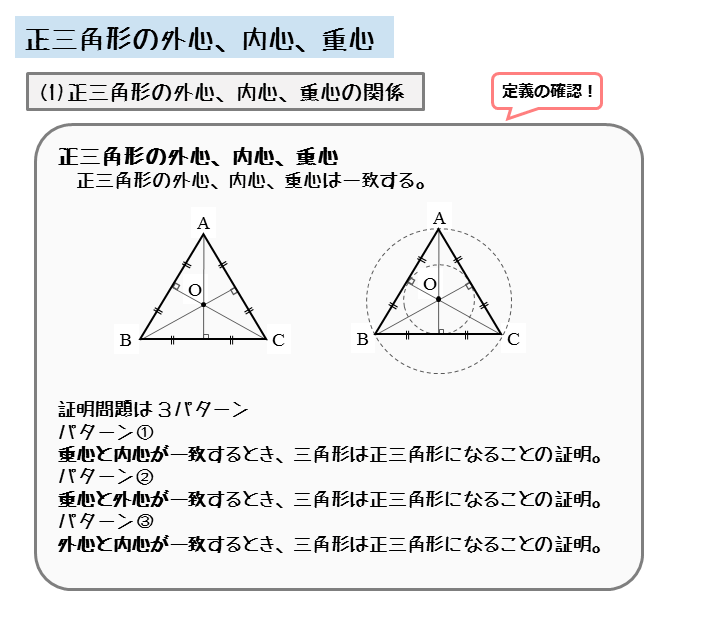
図形の性質 正三角形の外心 内心 重心について 日々是鍛錬 ひびこれたんれん
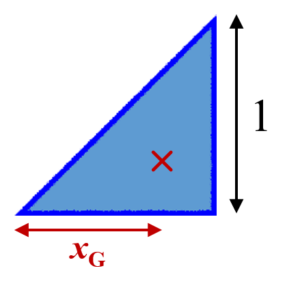
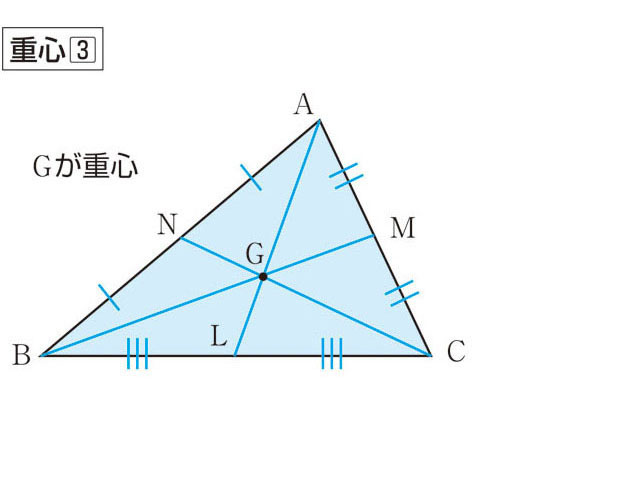
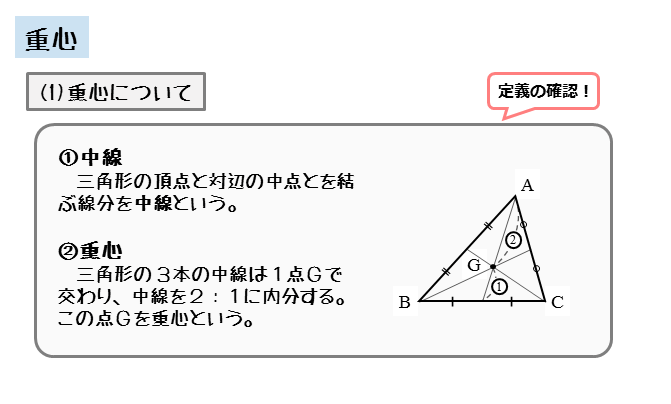
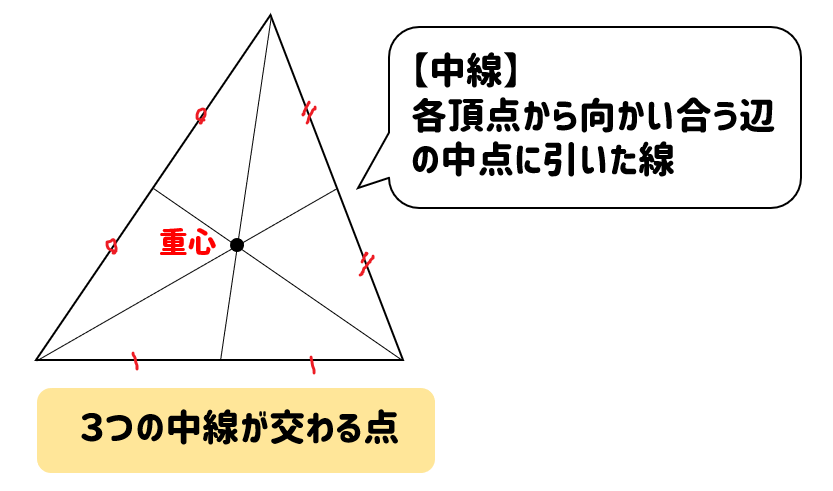
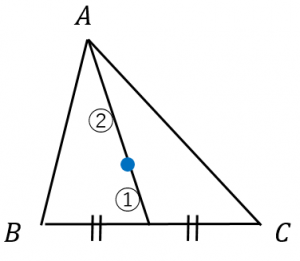
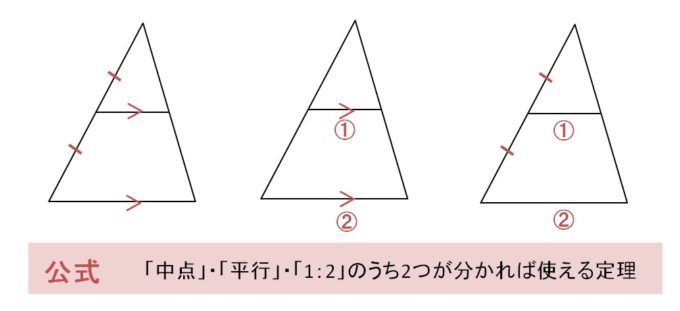
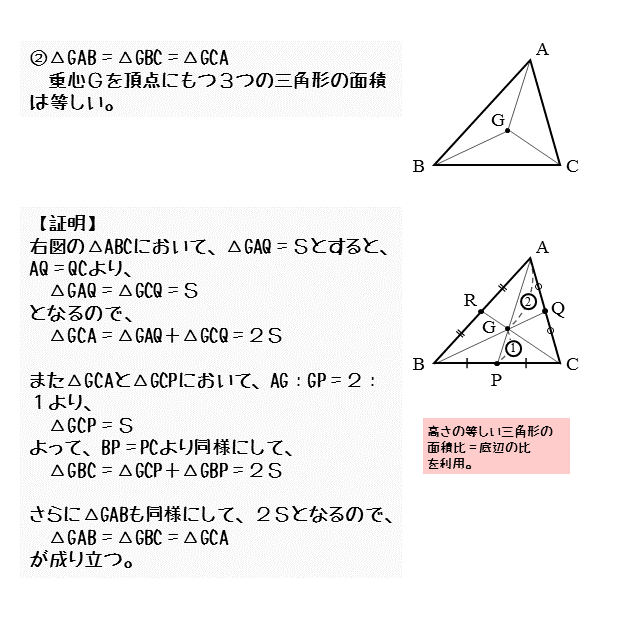
重心の求め方から応用問題まで徹底解説! │ 受験スタイル 例題付き重心って何? 重心の求め方から応用問題まで徹底解説! なんとなく物体の中心というイメージをもっているのではないでしょうか? 物理基礎でもあまり説明なく、そのように重心の特徴、問題の解き方 重心 とは、 3つの中線が交わる点 のことをいいます。 ※中線とは各頂点から向かい合う辺の中点に向かって引いた線のこと では、重心の特徴についてまとめておきましょう。 こんにちは、ウチダです。 今日は数学a「図形の性質」で習う 「三角形の重心」 の座標・位置ベクトルの求め方や、その公式の証明、また重心の重要な性質を利用した面積比を求める問題などをわかりやすく解説していきます。 また、記事の後半では、三角形
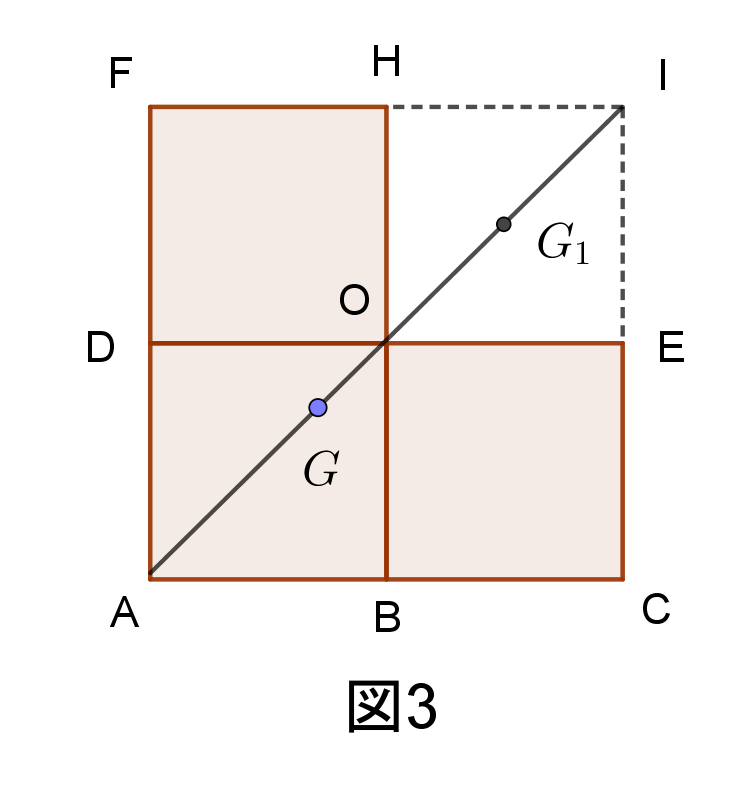
7角形の重心を計算しよう。 計算上、最後の3角形の面積計算のため、1番目の点座標を8番目にも設定します。 図4 多角形(ポリゴン)の重心計算 簡単ですね。重心の計算 (複雑形状の場合の考え方) 蓋形状がl 字型などになっている場合、単純形状に分割して部分ごとに重心位置を計算し、その合計で全体の重心を求めます。木板に鏡を付ける場合なども同様の考え方です。 try!建物の重心位置を正確に調べる方法 14年11月13日1118 Feng Sui 日本の多くの "風水診断士" さまは 建物の中心に 方位ラインを書いて 「鬼門がどうだ」 などという 診断手法をとります。 この手法は、 建築の専門家じゃなくても だれでも短時間に簡単に
図形 の 重心 の 求め 方のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 | ||
 | 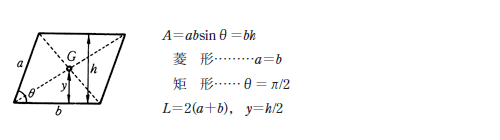 |  |
「図形 の 重心 の 求め 方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「図形 の 重心 の 求め 方」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 | ||
「図形 の 重心 の 求め 方」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 | ||
 |  | |
「図形 の 重心 の 求め 方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
「図形 の 重心 の 求め 方」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 |  |  |
「図形 の 重心 の 求め 方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「図形 の 重心 の 求め 方」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 | ||
「図形 の 重心 の 求め 方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「図形 の 重心 の 求め 方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 | ||
「図形 の 重心 の 求め 方」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 | 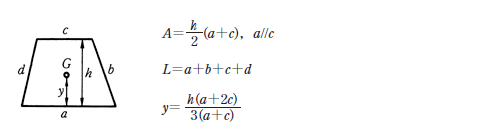 | |
 |  | |
「図形 の 重心 の 求め 方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |
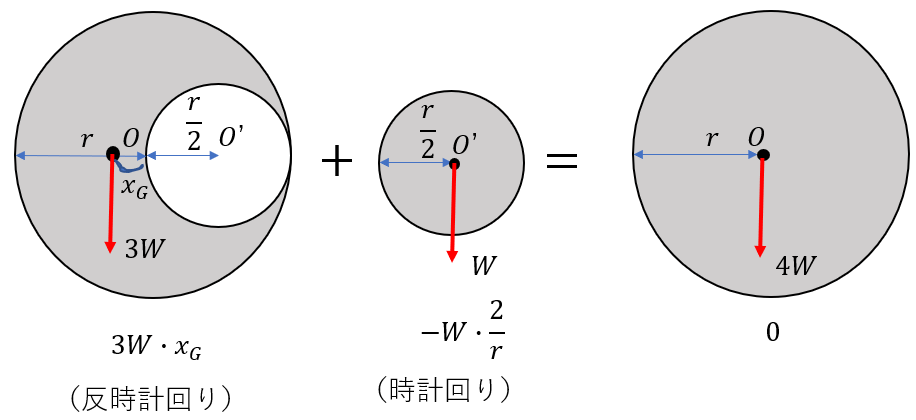
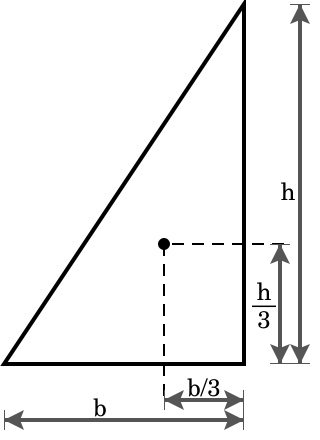
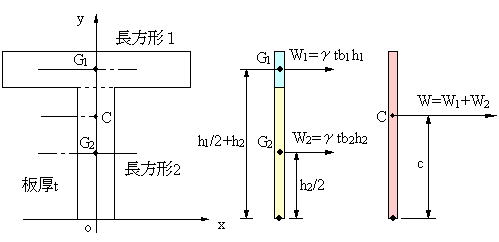
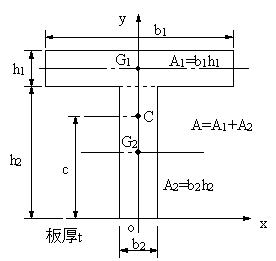
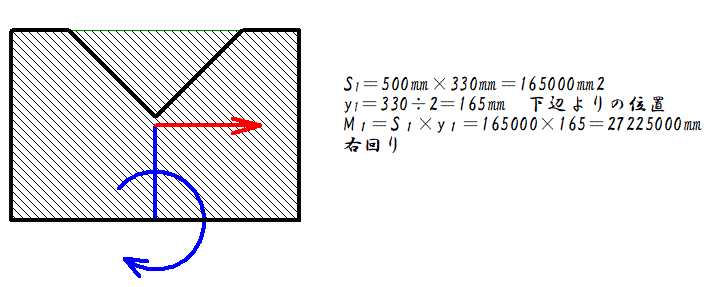
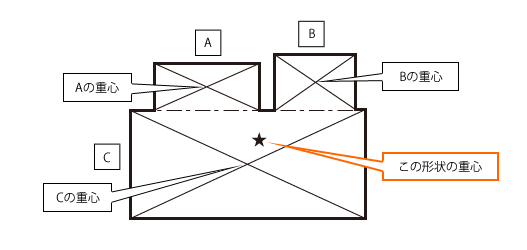
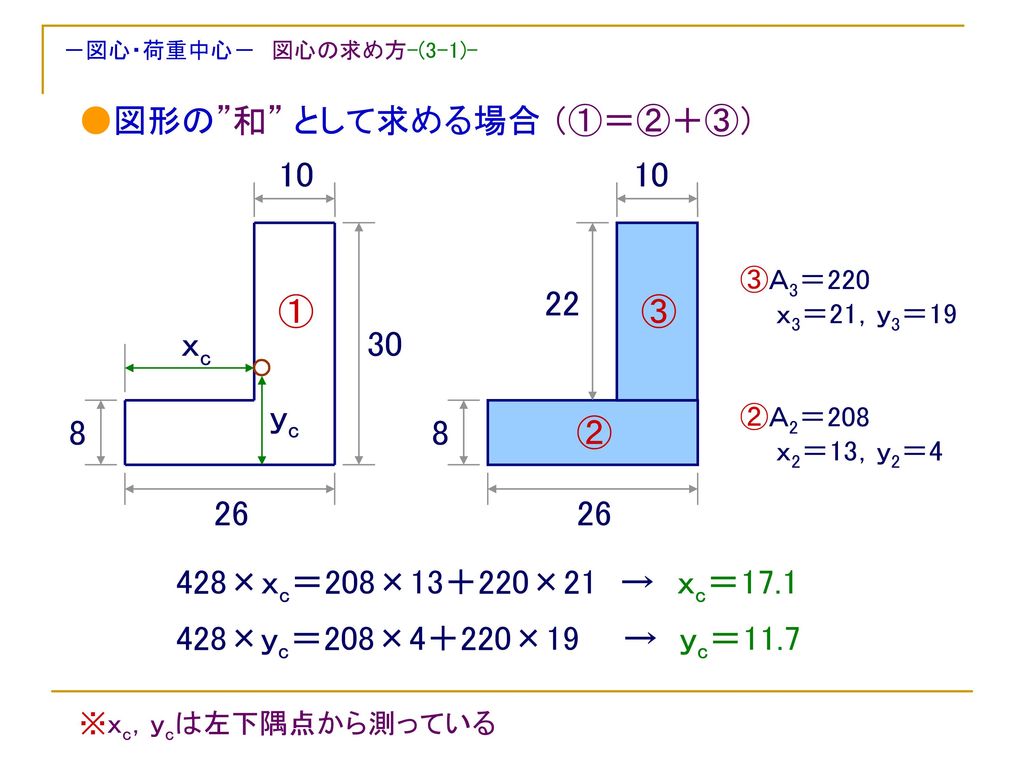
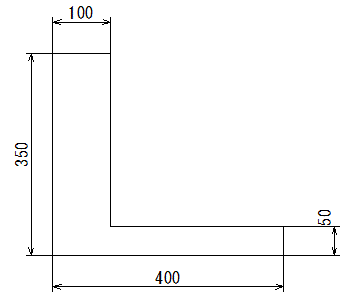
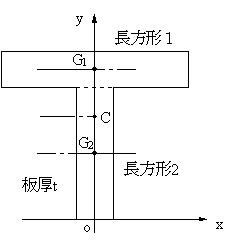
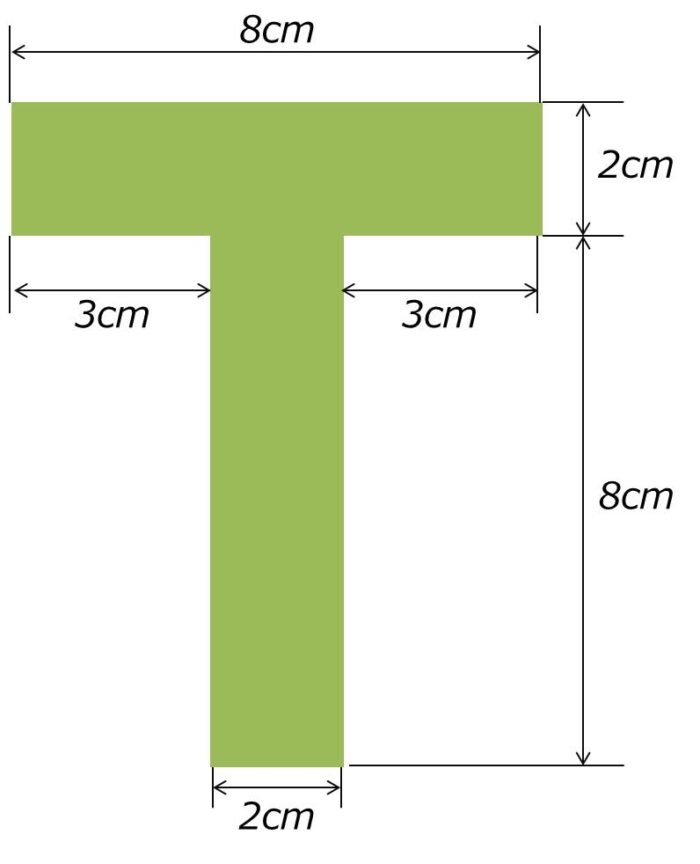
となる。作用点l 0 が重心の位置で、断面が一様な棒の場合は中点である。 T型の場合 図形の形状が、重心の位置が既知の図形に分解できるときにはそれぞれの面積と位置から合成することにより全体の形状の重心位置が求められます。図形の重心に対する感覚を豊かにする教材の提案 165 4.指導の展開 (ねらい)長方形の重心を見つける活動を通して,重心の求め方を理解し,それを応用してL字型図形の 重心を求めることができる。※授業内では「重心」を「つり下げられる点」と表現する。
Incoming Term: 図形 の 重心 の 求め 方,
Komentar
Posting Komentar